Dem B vs C Test nach Shainin gehen in der Regel Untersuchungen voraus, um die Vielzahl von möglichen Baugruppen, Komponenten, Variablen und Stellgrößen einzuengen. Wertvolle Werkzeuge sind hierbei Komponententausch, Variablenvergleich nach Shainin oder der Versuchsplanung nach Shainin. Nicht selten werden die Shainin-Techniken um weitere Methoden der Problem-Formulierung ergänzt wie z.B. SIPOC, Ishikawa-Diagramm, Mind Mapping oder 5W-Fragetechnik. Bild 1 gibt einen Überblick, wie diese Untersuchungen zusammenwirken.

Da Shainin größten Wert auf eine zielgerichtete, effektive und effiziente Vorgehensweise legte, kommen seine Methoden mit sehr wenigen repräsentativen Versuchen aus. Gerade deswegen ist es am Ende der Optimierung wichtig, die Belastbarkeit der Anpassungen festzustellen und zu dokumentieren. Dies ist ein wichtiger Punkt, der leider oftmals in der Euphorie über die gewonnenen Erkenntnisse untergeht.

Für diesen nachfolgenden Test dienen nur noch die sogenannten Red X zur Differenzierung, d.h. die mithilfe der Shainin Techniken identifizierten kritischen Einflussfakturen. Es geht nun darum, zu verifizieren, ob die in den vorangegangenen Tests gewonnen Erkenntnisse tatsächlich eine nachhaltige Verbesserung darstellen.

Je eindeutiger und quantifizierbarer die Effekte durch die Red X ausfallen, desto leichter lassen sich diese auch statistisch bewerten. Schwierig wird es immer dann, wenn die Verbesserungen marginal sind oder die Einsortierung der Qualitätslage einer subjektiven Einschätzung unterliegt. Beispiele für solche parametrisch nicht erfassbaren Kriterien sind: Geschmack des mit einem Kaffeevollautomaten gebrühten Espressos, visueller Eindruck einer PKW-Lackierung abhängig von Einfallswinkel und Beleuchtungssituation, Geruch eines Neuwagens, Klangqualität eines Soundsystems.

Ist die Verbesserung signifikant?

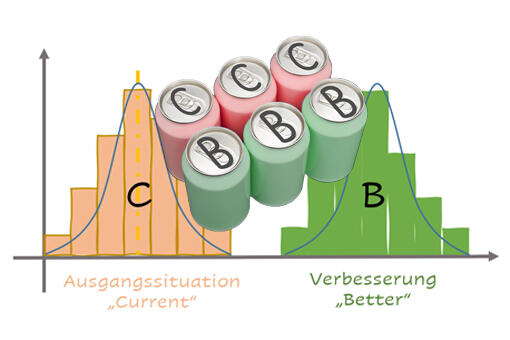
Bild 2 zeigt schematisch mögliche statistische Bedingungen für die Validierung einer Verbesserung. Dargestellt sind die jeweiligen Häufigkeitsverteilungen der als Kriterium dienenden Messgröße. Die orange gefärbte und mit "C" bezeichnete Häufigkeitsverteilung beschreibt die Ausgangssituation (current situation), die grün gefärbte und mit "B" bezeichnete Häufigkeitsverteilung die verbesserte Konfiguration.

Im Idealfall zeigen die Messwerte der Ausgangssituation und des optimierten Zustands Häufigkeitsverteilungen wie im oberen Diagramm von Bild 2: Der Abstand ihrer Mittelwerte ist signifikant größer als ihre Streuung.

Das untere Diagramm von Bild 2 zeigt weitere mögliche Häufigkeitsverteilungen: Im schlimmsten Fall decken sich die Häufigkeitsverteilungen, sodass objektiv gar keine Verbesserung besteht. Wohl aber kann es sein, dass einzelne Messungen eine Verbesserung vortäuschen.

Stichproben statt vollständiger Versuchsreihen sparen Kosten und Zeit

Für einen vollständigen Nachweis der Verbesserung wäre es somit erforderlich, die tatsächlichen Häufigkeitsverteilungen des Gütekriteriums für die B- und C-Konfigurationen experimentell zu bestimmen. Dies ist jedoch entweder sehr aufwendig oder kann sogar unmöglich sein, z.B. wenn es sich bei dem untersuchten Objekt um eine Großanlage handelt. Der B vs C Test nach Shainin zielt deshalb darauf ab, mit möglichst wenigen Testuntersuchungen herauszufinden, ob der erzielten Verbesserung ein echter Effekt zugrunde liegt.

Untersuchung auch bei kategorialer Bewertung möglich

Einen zusätzlichen Schwierigkeitsgrad stellt der Vergleich von Teilen dar, bei denen das Qualitätskriterium keine kontinuierliche Größe ist, sondern die in Kategorien wie "gut" und "schlecht" verglichen werden (Bild 3). Diese Kategorien lassen sich nicht mit gewohnten Untersuchungen wie z.B. T-Tests untersuchen, da "gut" und "schlecht" sich nur durch zwei Ausprägungen ohne Übergang darstellen lassen. Kategoriale Unterteilungen mit mehreren Kategorien sind mitunter ebenfalls schwierig zu untersuchen, da der Abstand zwischen den Gruppen oftmals nicht äquidistant ausgelegt bzw. bestimmt (gemessen) sondern nur beurteilt werden kann. Hierbei werden dann Methoden wie das Ranking angewandt, um Teile miteinander vergleichen zu können.

Wenn z.B. eine Stichprobe von Bauteilen mit nur zwei Ausprägungen (gut, schlecht) miteinander verglichen werden sollen, so entstehen oftmals zwischen den Produktverantwortlichen Endlosdiskussion zu Grad der Ausprägung, repräsentativer Stichprobenmenge und der daraus resultierenden Unterscheid- und Vergleichbarkeit von Referenz- oder Grenzmustern.

Für diese Anwendungen entwickelte Shainin vergleichende parameterfreie Bewertungen. Der Begriff "parameterfrei" bezeichnet hier den Umstand, dass statt quantifizierbarer Messwerte auch vergleichende Bewertungen oder Rangfolgen vorliegen können. So würden Versuchspersonen z.B. den Innengeruch mehrerer Test-PKWs nach einem Ranking sortieren und nicht versuchen, ihre Geruchsempfindung quantitativ zu formulieren. Diese Art von Tests ermöglicht es auch, sehr kleine Gruppen mit unterschiedlichen Bewertungen / Ausprägungen miteinander zu vergleichen. Das Ergebnis des Tests ist eine Wahrscheinlichkeit, inwiefern sich die Gruppen unterscheiden (z.B. die Verbesserung des Wagen-Innengeruchs anhand von je drei PKWs mit und ohne Verbesserung).

Schritt 1: Legen Sie den angestrebten Vertrauensbereich fest!

Um ein aussagekräftiges Ergebnis aus der Untersuchung abzuleiten, ist es erforderlich, entsprechende Mengen an Bauteilen mit den verschiedenen Ausprägungen zu untersuchen. Aus Tabelle 1 können Sie entnehmen, wie viele Bauteile jeder Ausprägung erforderlich sind, um den von Ihnen gewählten Vertrauensbereich zu erfüllen. In der Literatur gibt es noch wesentlich umfangreichere Tabellen, die insbesondere unterschiedliche Anzahlen von B- und C-Teilen aufführen, um bestimmte Vertrauensbereiche zu erziehen. Diese mitunter asymmetrischen Anzahlen sind dann sinnvoll, wenn die Bereitstellung oder das Testen von B- und C-Teilen große Kostenunterschiede aufweist. Dies kann z.B. der Fall sein, wenn die verbesserten Teile mit hohem Aufwand erstellt werden müssen oder von der alten Konfiguration nur noch wenige Teile vorhanden sind.

Der Vertrauensbereich "ρ" ist die Wahrscheinlichkeit der Annahme, dass die verbesserte Variante "B" tatsächlich besser ist als die bisher verwendete Variante "C". Das sogenannte α-Risiko ist das verbleibende Restrisiko, dass die Annahme falsch ist. Dieses Risiko wird auch als die Irrtumswahrscheinlichkeit angegeben und berechnet sich aus dem Vertrauensbereich: α-Risiko = 1-ρ.

Wenn es darum geht, die Verbesserung von Bauteilen mit geringstmöglichem Aufwand zu bewerten, so müssen hierfür mindestens zwei Bauteile C unter alten Bedingungen und zwei Bauteile B unter verbesserten Bedingungen produziert werden. Ist nun das schlechteste Bauteil der B-Gruppe besser als das beste Bauteil der C-Gruppe so kann mit einer Sicherheit von 83,3% darauf geschlossen werden, dass eine Verbesserung erzielt worden ist. Bei herkömmlichem Test der statistischen Prozesskontrolle müssten hierfür größere Gesamtheiten an Teilen für eine entsprechende Sicherheit ausgewertet werden. Der statistische Ansatz von Shainin beruht auf kombinatorischen Überlegungen, die ich im Folgenden kurz anhand des Zahlenbeispiels mit zwei B-Teilen und zwei C-Teilen erläutere.

Die Grundannahme ist, dass sich Unterschiede zwischen B- und C-Teilen rein statistisch ergeben würden, falls die vorgenommenen Veränderungen in Wirklichkeit keine Verbesserung bewirken würden. Dies entspräche der Situation in Bild 2 links unten. Die Frage ist nun: Wie hoch ist die Wahrscheinlichkeit, dass beide B-Teile in der Messung besser als beide C-Teile abschneiden, obwohl beide Konfigurationen in ihrer statistischen Gesamtheit gleichwertig sind? Um diese Frage zu beantworten, müssen wir ganz einfach die insgesamt vier Teile (zwei B, zwei C) in alle möglichen Reihenfolgen bringen. Dabei ist es egal, in welcher Reihenfolge jeweils die beiden B- und die beiden C-Teile vorliegen.

Anschaulich zeigt Bild 4 alle sechs möglichen Kombinationen. Mathematisch lässt sich die Anzahl der Kombinationen zweier Mengen von nicht-unterscheidbaren Elementen mit folgender Formel berechnen:

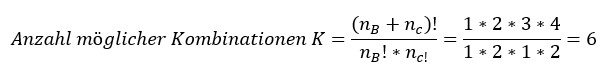
D.h. es gibt genau sechs Möglichkeiten, B- und C-Teile in beliebiger Anordnung übereinander anzuordnen. Nur bei einer dieser Anordnungen sind alle B-Teile oben im guten Bereich und alle C-Teile zufällig unten im schlechteren Bereich angeordnet. Trifft die Annahme zu, dass es gar keine Verbesserung gegeben hat, dann wird der B vs C Test also lediglich mit einer Wahrscheinlichkeit von 16,7% versagen und vortäuschen, dass die B-Konfiguration besser ist.

Umgekehrt bedeutet dies: Ist das schlechteste Bauteil der B-Gruppe besser als das beste Bauteil der C-Gruppe so kann mit einer 83,3% Sicherheit darauf geschlossen werden, dass eine Verbesserung erzielt worden ist.

Die Frage ist nun, mit welcher Sicherheit Sie die durchgeführte Verbesserungsmaßnahme validieren wollen. Bereits mit jeweils drei B- und C-Teilen – dem berühmten Shainin's Six Pack Test – wissen Sie dies mit einer Wahrscheinlichkeit von 95%! Es ist letztlich eine wirtschaftliche Entscheidung, wie hoch die Risikobewertung einer Fehlentscheidung ist im Vergleich zu den Aufwänden für die durchzuführenden Tests.