
Amortisationsdauer
Amortisationsdauer
Berechnungsbeispiele im Projektmanagement
Investitionsentscheidung für ein Projekt, Beispiel Software-Entwicklung
Zu beurteilen ist ein Projekt, das eine Software zur automatisierten Bestellverwaltung entwickeln und einführen soll. Diese soll die manuelle Bestellverwaltung ablösen. Die Projektkosten wurden mit 14.000 Euro geschätzt; laufende Kosten nach Inbetriebnahme des neuen Systems entstehen durch Wartung und Administration in Höhe von 500 EUR pro Jahr. Die aktuellen Betriebskosten durch den derzeitigen Bestellprozess im Unternehmen betragen pro Jahr rund 10.000 Euro. In Zukunft sollen sie auf 5.000 Euro jährlich reduziert werden.
Dabei werden die Einzahlungen durch die Einsparungen der aktuellen Betriebskosten dargestellt. Es wird vermutet, dass sich die Einsparung erst im dritten Jahr in voller Höhe ergibt. Tabelle 1 listet die Ein- und Auszahlungen in den kommenden Perioden auf.
| Jahr | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Auszahlungen in € | -14.000 | -500 | -500 | -500 | -500 |
| Einzahlungen in € | - | 2.500 | 3500 | 5.000 | 5.000 |
| Kumulierte Summe in € | -14.000 | -12.000 | -9.000 | -4.500 | - |
Anhand Tabelle 1 zeigt sich eine Amortisationsdauer von 4 Jahren für das Software-Entwicklungsprojekt. Diese sogenannte statische Berechnung (siehe Amortisationsrechnung ) erfolgt gemäß Formel 1:
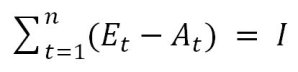
Formel 1: Statische Berechnung der Amortisationsdauer
E steht für Einzahlungsüberschüsse, A für Auszahlungen jeweils für die Periode t. I steht für den getätigten Investitionsbetrag und n für die Anzahl der Perioden.
Finanzierungsplanung, Beispiel Maschinenkonstruktion
Projektgegenstand ist der Bau einer Sondermaschine. Als Investition werden die gesamten bis zum Betrieb der Maschine aufgelaufenen Ausgaben des Projekts für Konstruktion und Bau der Maschine betrachtet, zuzüglich der Baunebenkosten für Fundamente etc. (Zeile Auszahlungen, Spalte 0). Die laufenden Betriebskosten werden in den Spalten der Jahre 1 bis 4 ergänzt.
Die erwarteten Einzahlungen ergeben sich dann rechnerisch aus den Erlösen, die durch den Einsatz der Maschine in der Produktion von Gütern erzielt werden können, ggf. über die betriebliche Leistungsverrechnung. Die Einzahlungsüberschüsse ergeben sich daraus durch den Abzug der laufenden Betriebskosten, der Abschreibungen und der Finanzierungskosten für den Kredit.
Für die Berechnung eignet sich das dynamische Verfahren für die Berechnung der Amortisationsdauer, das einen Kalkulationszinssatz mit einbezieht Berechnung (siehe Amortisationsrechnung ).
Die Einzahlungsüberschüsse werden also aus heutiger Sicht umso niedriger bewertet, je weiter sie in der Zukunft liegen. Wird ein Kalkulationssatz von 5% angenommen, so amortisiert sich die Investition in fünf Perioden, wie Tabelle 2 zeigt.
| Jahr | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Auszahlungen in € | -140.000 | -5.000 | -5.000 | -5.000 | -5.000 | -5.000 |
| Einzahlungen in € | - | 40.000 | 40.000 | 40.000 | 40.000 | 40.000 |
| Überschüsse bewertet mit Kalkulationszins 5% in € | - | 33.333 | 31.746 | 30.234 | 28.795 | 27.423 |
| Kumulierte Summe in € | -140.000 | -106.667 | -74.921 | -44.686 | -15.892 | 11.532 |
Die Formel für die Berechnung der dynamischen Amortisationsdauer lautet:
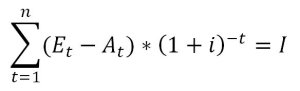
Formel 2: Dynamische Berechnung der Amortisationsdauer
In Formel 2 stehen wieder E für Einzahlungsüberschüsse, A für Auszahlungen jeweils für die Perioden t, I für den getätigten Investitionsbetrag, i für den Kalkulationssatz und n für die berechneten Perioden.


